2.1.6. Float upsampling factor:¶
Omitting the potential artifacts discussed in previous chapters, the process of upsampling a signal by a factor
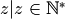 is rather simple. All it takes is adding the right number of zeros to the signal spectrum.
is rather simple. All it takes is adding the right number of zeros to the signal spectrum.
This being said, the right number of zeros might be hard to find (if at all) when 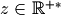 .
Assuming the input signal size is
.
Assuming the input signal size is 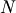 , and the user zooming factor is
, and the user zooming factor is 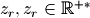 , then
the padding spectrum size must be
, then
the padding spectrum size must be 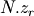 .
.
Chances are 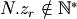 so the input signal has to be padded up to a size
so the input signal has to be padded up to a size
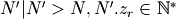 assuming such a
assuming such a 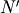 exists.
exists.
If it does, then it is easy to figure out how this padding could imply overhead.
If it does not, and the spectrum is padded up to a size 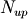 such that
such that
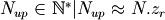 then the zooming factor actually
applied is
then the zooming factor actually
applied is 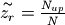 .
.
To make sure Sirius always applies the user required zooming factor, and not an approximation of it, Sirius requires the
user to set the input spacing, and the output one. Say the required zooming factor is 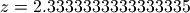 then the user must set input spacing to
then the user must set input spacing to 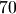 and output spacing to
and output spacing to 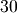 (no matter the unit here).
(no matter the unit here).
Sirius will then understand the zooming factor is 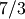 and so will upsample the input data by a factor
and so will upsample the input data by a factor 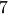 before decimating the output to keep only
before decimating the output to keep only 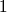 pixel out of
pixel out of 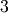 .
.
This process ensures the zooming factor is exactly the one required by the user. It shall be noted the decimation is a
safe process here and no aliasing will come from it. Indeed, the input spacing is 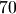 (again, no matter the unit),
so decimating from
(again, no matter the unit),
so decimating from 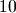 to
to 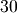 remains an aliasing free process since zooming from
remains an aliasing free process since zooming from 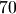 to
to 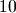 dit not add higher frequencies than the ones already contained in the original spectrum.
dit not add higher frequencies than the ones already contained in the original spectrum.
Note
If one has given Sirius a low-pass filter to control the way high frequencies are cut-off, Sirius assumes this
filter is sampled at the targeted resolution (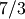 here). Because the zooming
factor will actually by
here). Because the zooming
factor will actually by 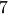 , Sirius will firstly upsample the filter by a factor
, Sirius will firstly upsample the filter by a factor 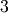 . This upsampling
is obviously done using Fourier zero padding. This is equivalent to a sinc convolution which shall be the perfect
way to upsample a continuous and rather smooth filter.
. This upsampling
is obviously done using Fourier zero padding. This is equivalent to a sinc convolution which shall be the perfect
way to upsample a continuous and rather smooth filter.